About The Electric Shocktopus

Shocktopus FAQ

Everything you wanted to know, but were afraid to ask the sparky cephalopod

Player-made Levels

You can make and share your own levels with the in-game editor. Find out how many spikes you can jump over, or what crazy puzzle you can make, or what the electric field looks like as it fringes around a capacitor. There is a whole slew of levels that people have already made and posted in the forums, and I encourage you to share yours, too! I always love seeing what players can make.

I try to play through all the levels that I hear about -- and I regularly post videos of me attempting particularly challenging/interesting ones. Check out the Feel Bad Friday videos on YouTube to see me struggle to 100% some tough levels. Who knows? Maybe your level will be next? Check out this classic FBF, where I play through Juggling:

Walkthrough

Having trouble beating the game? Well, then, if you insist... here is a walkthrough. Watch at your own spoiler-related peril.

Teacher Resources

Are you a teacher looking for resources? Well, first off, kudos to you for checking out a video game! On its own, The Electric Shocktopus isn't designed to teach all of Electromagnetism. It showcases a few key lessons about the topic, and makes players investigate the world by solving the physics-related puzzles. The game is built to be a standalone way to play around with the subject matter, and learn a thing or two.

But the game also fits well as a supplement to classroom instruction. Here are some examples of things your students can investigate:

Based on the Voltmeter in the game, what is the strength of the charges in Coulombs?
Based on how the Shocktopus moves, how strong is gravity?
Based on how the Shocktopus moves, what is the strength of *his* charge?
How about the strength of the magnetic fields?
Have the students make a level that shows off a concept (dipoles, shielding, capacitors, biot-savart law, etc)
Have them play the levels each other made!

If you do end up using the game as part of a classroom activity, I'd love to hear about it!

FAQ Answered

The Science

What am I learning here, really?

You are learning how to play the Electric Shocktopus. That's all the game tries to teach you.

It just so happens that in order to beat the game, you've got to play around with, and develop some intuition for, electromagnetism. You'll get experience interacting with Electric Fields, see how extra charges and conductors affect those fields. You'll twist and spin as you move through Magnetic Fields. So it turns out you'll need to learn a lot!

The game does not aim to replace a class on the subject. There are no walls of text, no math equations to solve. If you want to learn more about that side of Electromagnetism, I highly encourage you to do so. There are plenty of resources around.

What about the simulation is scientifically correct?

A whole bunch of stuff. The electric fields from charged particles and conductors are calculated quite accurately by the game. You can read more below, but it truly is an accurate depiction of electric fields. The magnetic fields are a bit more boolean (on or off), especially early on in the game. Not exactly something you'd find in the world, but it is a good model for understanding the fields.

Your character is acted on by three forces: electricity, magnetism, and gravity, and the game simulates all of these forces correctly. A charged particle (shocktopus) in an electric field will accelerate in the direction of that field by an amount proportional to the strength of the electric force. A moving charged particle will bend in a magnetic field, which you can figure out through the Right Hand Rule. And gravity, as it should, accelerates your Shocktopus down.

What is not scientifically correct?

There are a few reasons that your character doesn't act *exactly* like a charged particle would in the real world. One thing is that the Shocktopus can choose to move side to side - even when suspended in the air. And if you don't press 'go left' or 'go right', he activates his air brakes, and slows down his horizontal motion. Which, again, isn't quite like particles work. And it can lead to some neat methods of adding or removing energy from your Shocktopus.

Beyond that, the only other limit to the simulation is the roughness of the grid. The electric field is computed exactly at the vertices of the grid (the cells of the grid are the size of the tiles in the game). Anywhere between those vertices, the electric force is averaged. This is generally not noticeable, and speeds up the game a lot. One consequence, though, is that if you get extremely close to a charge (within half a tile's distance), the force hits a limit of how big it'll get. In the real world, the closer you got, the strong the force would be -- with *no* limit. So get right next to a charge, and from one frame to the next, your character might have flown off the screen. That wouldn't be too friendly to a game.

Why does the Shocktopus shoot lightning bolts?

Because it's awesome.

Hrm, no, let me try to justify this...

When he charges himself positively, he starts to get a bit of corona discharge off his pointy tentacles. Some of those lead to a dielectric breakdown of the air, and sparks. So there.

But, yeah, really just 'cause it's rad.

Electricity

How do you calculate the electric fields?

At the most basic level, calculating electric fields is really easy. The basis for it all is Coulomb's Law:

Basically, the electric field around a point charge is the strength of its charge divided by the square of the distance you are away from the charge. And there's some constants multiplied to the front so units/values all work out. The direction of a field is towards the charge when it's negative and away from the charge when it's positive. Pretty straightforward.

But there are many charges around! How do you deal with that?

Turns out, when you have more than one charge, the total electric field is just the sum of their individual fields. So calculate E from each charge by Coulomb's Law... and add 'em up. This is known, by the way, as the Superposition Principle.

Why does a conductor warp the electric field?

Coulomb's Law and the Superposition Principle basically give us everything we need to figure out an electric field, assuming we know where all the charges are. With conductors, this isn't the case.

A conductor is made up of a whole bunch of charges, and importantly, they can move. So if you put a chunk of copper in an electric field, positive charges will be attracted towards one end, and negative charges to the other. (Only the negative charges - electrons - really move, though.) These charges move until they settle down to a stable arrangement. One where they are no longer pushed or pulled. And the question becomes... well... what is that arrangement?

How do you compute that?!?

In physics class, we often calculate problems like this... but only when they are extremely basic. So a point charge sitting next to a flat conductor that's an infinite plane. Or maybe the conductor is a sphere. In those cases, we can use some tricks (like image charges) to figure out what the field will look like.

But in this game, things *aren't* basic. You can place conductors and charges wherever you'd like, and that means we can't use those simple tricks.

In the game, I use the Relaxation Method. (Don't let the name fool you, it has brought me many hours of frustration.) Basically you set up an initial guess of what the voltages should be in the level.

Voltage is, I should mention, related to the Electric Field. If we know one of these everywhere in the level, we can know the other, too.

The thing is, our initial guess isn't right. It's just a guess. What the Relaxation Method gives us is a way to take a guess, and make it better. With our grid of starting voltages, we then turn a mathematical crank, and get a whole new, slightly better, guess. And we can do this again and again, each time getting closer to the correct solution

It takes a while for our answer to get 'nearly correct', though. In some levels, this can take a few thousand iterations. But for all that work, we can calculate the Electric Field.

If you want to know more about how the Relaxation Method really works, here's a good place to start.

How strong are the charges in the game?

I'll leave that as an exercise for the player.

Magnetism

What are the South and North magnet tiles, really?

They are a quick-and-dirty way of drawing a magnetic field. A 'South' block, represented by the letter 'S' or an 'x', represents a magnetic field pointing *into* the screen. Roughly what you'd get if there was the 'South' end of a magnet just behind the screen. A 'N' or 'dot' is roughly what you'd get with a 'North' pole of a magnet behind your screen -- a magnetic field pointing *out* towards your face.

Why do I move in a curved path in a magnetic field?

To figure out the Magnetic Force that pushes on a charge, we compute:

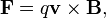
(This is the magnetic piece of the Lorentz Force)

F is the force we get, q is the value of the charge, v is the velocity, and B is the magnetic field.

So the force on a charge gets bigger as the magnetic field gets bigger. Or if you have a stronger charge. Or if the charge is going faster.

The 'x' in the equation is no simple multiplication, though, it is called a 'cross product.' This is important to help us find the *direction* of the force. In order to find which way the force pushes the charge, we need to do use the Right Hand Rule.

My favorite way to describe it: take your right hand, hold it out open in front of you. Point your index finger in the direction of the velocity. Then bend your other three fingers in the direction of the magnetic field. (You may need to move your hand around a bit to make this work.) If you've done it right, your thumb (sticking out) should be pointing in the direction the magnetic force would push a positive charge. (For a negative charge, it gets pushed the opposite way, due to the minus sign.)

Why does this make you move in a curve? Well, the force, you'll notice, is pointing perpendicularly to your velocity. Imagine a puck moving across an air hockey table in a straight line. Push on it sideways (perpendicular to its motion), and you'll deflect it. In the case of magnetism, the force on a particle is always at 90 degrees from the direction the particle is moving, so you keep getting deflection. A moving charged particle would this start to spin in a circle.

And why do I make those loop-de-loops?

You, the Shocktopus, do not move in a circle, though, and the reason is that magnetism is not the only force pushing on you. Gravity is still around. And in some levels, electric forces are there, too. When gravity is added into the picture, you start making loops and drifting off to the side. Your path is a cycloid, which is a specific type of loop-de-loop. (And it sounds much more scientific, eh?) This topic is really cool, and I encourage you to learn more about it.

One thing I will note about the cycloid path is this: remember that magnetic fields don't add or take away any energy from you (unlike electric fields). So if you're moving around in one, you wouldn't suddenly speed up and go faster... or slow down, for that matter. If you look at your cycloid path you make, notice how your energy is conserved. If there's only gravity and magnetism, you'll drift along, always looping between the same heights. And at your highest point you'll go slower (you've given some of your kinetic energy to increase your gravitational potential) and at your lowest point, you'll go faster (since some of your gravitational potential energy has been converted to kinetic energy).

How strong is this magnetic field?

This is left as an exercise for the player.

The Game

I'm stuck on a level!

Not a question. But check out the walkthrough *here*.

The game is intended to be tough, so keep that in mind. Remember: you don't need to get all the stars.

I found a bug in the game

Let me know about it! I try to track down as many problems as possible before a game launches, but there are inevitably some issues that slip through. You can reach me at the email address at the bottom of this page.

Who made the sound?

Isn't it great? The music was created by Brian Allen Holmes, who worked some real magic. Take a listen to his other stuff. The Sound Design was by Kevin Notar -- he made the squishy Shocktopus sounds you hear, the chimes as you collect stars, the seagulls in the background. The music and sfx really added a great dimension to the game.

I made an awesome level. How can I share it with people?

There is a Level Editor in the game, and we've seen some amazing levels come out of it. You can share a level by sending the level code (a string of letters and numbers) to people through email, Facebook, or whatever. They'll be able to paste the code in and play the level. If you want to share your level with the TestTubeGames community, or see what other people have made, head on over to the forums.

Home	Blog	Games	Forums	About
		.
		Agent Higgs 2		Press Kit
		Gravity Simulator		Privacy Policy
		The Electric Shocktopus		Merch
		Velocity Raptor		-
		The Fittest 2		Support Free Resources
		Bond Breaker
		Black Hole Explorer
		-more-